How Computing Power Can Help Us Look Deep Within Our Bodies, and Even the Earth

Share
CAT scans, MRI, ultrasound. We are all pretty used to having machines — and doctors — peering into our bodies for a whole range of reasons. This equipment can help diagnose diseases, pinpoint injuries, or give expectant parents the first glimpse of their child.
As computational power has exploded in the past half-century, it has enabled a parallel expansion in the capabilities of these computer-aided imaging systems. What used to be pictures of two-dimensional “slices” have been assembled into high-resolution three-dimensional reconstructions. Stationary pictures of yesteryear are today’s real-time video of a beating heart. The advances have been truly revolutionary.
Though different in their details, X-ray computed tomography, ultrasound and even MRI have a lot in common. The images produced by each of these systems derive from an elegant interplay of sensors, physics and computation. They do not operate like a digital camera, where the data captured by the sensor are basically identical to the image produced. Rather, a lot of processing must be applied to the the raw data collected by a CAT scanner, MRI machine or ultrasound system to produce before it the images needed for a doctor to make a diagnosis. Sophisticated algorithms based on the underlying physics of the sensing process are required to put Humpty Dumpty back together again.
Early scanning methods
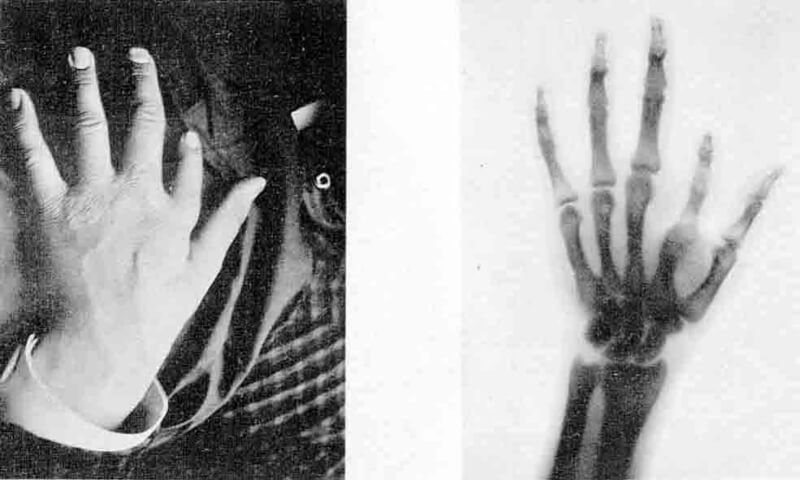
One of the first published X-rays (at right, with normal view of the hand at left), from 1896. Image credit: Albert Londe/Wikimedia Commons
A modern hand X-ray. Image credit: golanlevin/Flickr, CC BY
Though we use X-rays in some cutting-edge imaging techniques, X-ray imaging actually dates back to the late 1800s. The shadowlike contrast in X-ray images, or projections, shows the density of the material between the X-ray source and the data sensor. (In the past this was a piece of X-ray film, but today is usually a digital detector.) Dense objects, such as bones, absorb and scatter many more X-ray photons than skin, muscle or other soft tissue, which appear darker in the projections.
But then in the early 1970s, X-ray CAT (which stands for Computerized Axial Tomography) scans were developed. Rather than taking just a single X-ray image from one angle, a CAT system rotates the X-ray sources and detectors to collect many images from different angles — a process known as tomography.
The difficulty is how to take all the data, from all those X-rays from so many different angles, and get a computer to properly assemble them into 3D images of, say, a person’s hand, as in the video above. That problem had a mathematical solution that had been studied by the Austrian mathematician Johann Radon in 1917 and rediscovered by the American physicist (and Tufts professor) Allan Cormack in the 1960s. Using Cormack’s work, Godfrey Hounsfield, an English electrical engineer, was the first to demonstrate a working CAT scanner in 1971. For their work on CAT, Cormack and Hounsfield received the 1979 Nobel Prize in Medicine.
Extending the role of computers
Until quite recently, these processing methods had more or less been constant since the 1970s and 1980s. Today, additional medical needs — and more powerful computers — are driving big changes. There is increased interest in CT systems that minimize X-ray exposure, yielding high-quality images from fewer images. In addition, certain uses, such as breast imaging, encounter physical constraints on how much access the imager can have to the body part. This requires scanning from only a very limited set of angles around the subject. These situations have led to research into what are called “tomosynthesis” systems — in which limited data are interpreted by computers to form fuller images.
Similar problems arise, for example, in the context of imaging the ground to see what objects — such as pollutants, land mines or oil deposits — are hidden beneath our feet. In many cases, all we can do is send signals from the surface, or drill a few holes to take sampling measurements. Security scanning in airports is constrained by cost and time, so those X-ray systems can take only a few images.
In these and a host of other fields, we are faced with less overall data, which means the Cormack-Hounsfield mathematics can’t work properly to form images. The effort to solve these problems has led to the rise of a new area of research, “computational sensing,” in which sensors, physics and computers are being brought together in new ways.
Sometimes this involves applying more computer processing power to the same data. In other cases, hardware engineers designing the equipment work closely with the mathematicians figuring out how best to analyze the data provided. Together these systems can provide new capabilities that hold the promise of major changes in many research areas.
Be Part of the Future
Sign up to receive top stories about groundbreaking technologies and visionary thinkers from SingularityHub.


New scanning capabilities
One example of this potential is in bio-optics, the use of light to look deep within the human body. While visible light does not penetrate far into tissue, anyone who has shone a red laser pointer into their finger knows that red light does in fact make it through at least a couple of centimeters. Infrared light penetrates even farther into human tissue. This capability opens up entirely new ways to image the body than X-ray, MRI or ultrasound.
Again, it takes computing power to move from those images into a unified 3D portrayal of the body part being scanned. But the calculations are much more difficult because the way in which light interacts with tissue is far more complex than X-rays.
As a result we need to use a different method from that pioneered by Cormack in which X-ray data are, more or less, directly turned into images of the body’s density. Now we construct an algorithm that follows a process over and over, feeding the result from one iteration back as input of the next.
The process starts by having the computer guess an image of the optical properties of the body area being scanned. Then it uses a computer model to calculate what data from the scanner would yield that image. Perhaps unsurprisingly, the initial guess is generally not so good: the calculated data don’t match the actual scans.
When that happens, the computer goes back and refines its guess of the image, recalculates the data associated with this guess and again compares with the actual scan results. While the algorithm guarantees that the match will be better, it is still likely that there will be room for improvement. So the process continues, and the computer generates a new and more improved guess.
Over time, its guesses get better and better: it creates output that looks more and more like the data collected by the actual scanner. Once this match is close enough, the algorithm provides the final image as a result for examination by the doctor or other professional.
The new frontiers of this type of research are still being explored. In the last 15 years or so, researchers — including my Tufts colleague Professor Sergio Fantini — have explored many potential uses of infrared light, such as detecting breast cancer, functional brain imaging and drug discovery. Combining “big data” and “big physics” requires a close collaboration among electrical and biomedical engineers as well as mathematicians and doctors. As we’re able to develop these techniques — both mathematical and technological — we’re hoping to make major advances in the coming years, improving how we all live.
Eric Miller, Professor and Chair of Electrical and Computer Engineering, Adjunct Professor of Computer Science, Adjunct Professor of Biomedical Engineering, Tufts University
This article was originally published on The Conversation. Read the original article.
Banner image credit: Shutterstock.com
The research in our group is focused on the development and analysis of signal and image processing algorithms for solving what are known as inverse problems. Examples of such problems can be found in fields ranging from image restoration and medical imaging to geophysical exploration and non-destructive testing. Many of the problems in which we are interested are closely related to some underlying physical process such as wave propagation or heat diffusion and our algorithms are designed to incorporate in some reasonable way, the appropriate mathematical models (i.e. the wave equation, the Helmholtz equation, the diffusion equation, etc.).
Related Articles

How Scientists Are Growing Computers From Human Brain Cells—and Why They Want to Keep Doing It

AI Companies Are Betting Billions on AI Scaling Laws. Will Their Wager Pay Off?
These Brain Implants Are Smaller Than Cells and Can Be Injected Into Veins
What we’re reading