This is the third in a four-part series looking at the big ideas in Ray Kurzweil’s book The Singularity Is Near. Be sure to read the other articles:
- Will the End of Moore’s Law Halt Computing’s Exponential Rise?
- Technology Feels Like It’s Accelerating — Because It Actually Is
- Ray Kurzweil Predicts Three Technologies Will Define Our Future
“The future is widely misunderstood. Our forebears expected it to be pretty much like their present, which had been pretty much like their past.” –Ray Kurzweil, The Singularity Is Near
We humans aren’t great predictors of the future. For most of history, our experience has been “local and linear.” Not much change occurred generation to generation: We used the same tools, ate the same meals, lived in the same general place.

As a result, we’ve developed an intuitive outlook of the future akin to how we approach a staircase—having climbed a number of steps, our prediction of what’s to come is simply steps followed by more steps, with each day expected to be roughly like the last.
But, as Ray Kurzweil describes in The Singularity Is Near, the rapid growth of technology is actually accelerating progress across a host of domains. This has led to unexpected degrees of technological and social change occurring not only between generations, but within them.
Against our intuition, today the future is unfolding not linearly but exponentially, making it challenging to predict just what will happen next and when. This is why the pace of technological progress tends to surprise us, and we find ourselves in situations like this:
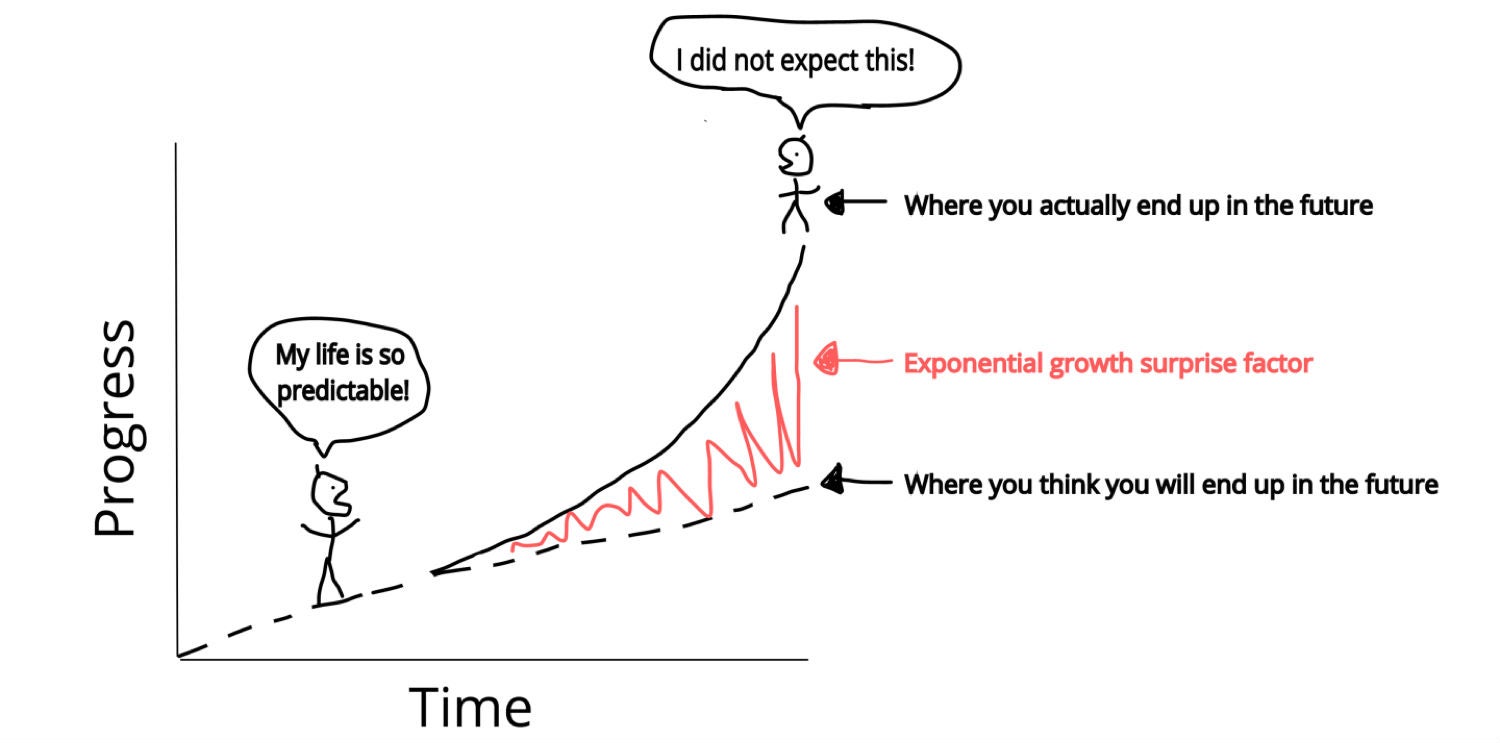
How do we prepare for a future tracking to exponential trends, if we aren’t accustomed to thinking this way? Let’s start with the basics of exponential growth.
What is exponential growth?
Unlike linear growth, which results from repeatedly adding a constant, exponential growth is the repeated multiplication of a constant. This is why linear growth produces a stable straight line over time, but exponential growth skyrockets.
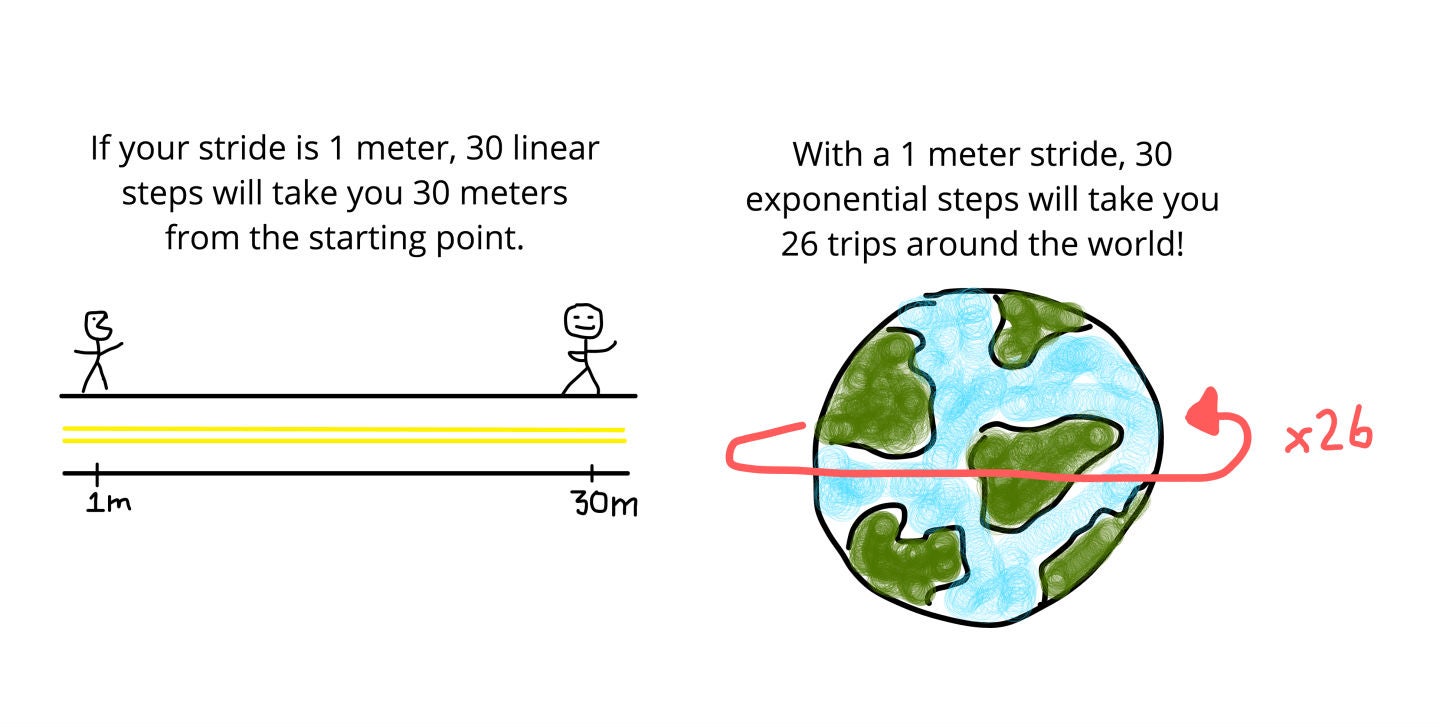
Here’s another way to think about it: imagine you are going to walk down a road taking steps a meter in length. You take 6 steps, and you’ve progressed six meters (1, 2, 3, 4, 5, 6). After 24 more steps, you’re 30 meters from where you began. It’s easy to predict where 30 more steps will get you—that’s the simplicity of linear growth.
However, setting anatomy aside, imagine you could double the length of your stride. Now when you take six steps, you’ve actually progressed 32 meters (1, 2, 4, 8, 16, 32), which is significantly more than the 6 meters you’d move with equal steps. Amazingly, by step number 30, doubling your stride will put you a billion meters from where you started, a distance equal to twenty-six trips around the world.
That’s the surprising, unintuitive power of exponential growth.
Exponential growth is deceptive, then explosive
What’s interesting about exponential growth is that when you double your stride, you progress the same distance with each step as all the previous steps combined. Before you hit a billion miles at step 30, you’re at 500 million miles at step 29. That means that any of your previous steps look minuscule compared with the last few steps of explosive growth, and most of the growth happens over a relatively short period of time.
Another example: let’s say you want to get to a certain location and you’re going to double your stride again to get there. Progress toward your destination appears distant at one percent of the way there, but in fact, you’re only seven steps (or doublings) away—and much of all that progress happens in the last step.
The point is we often miss exponential trends in their early stages because the initial pace of exponential growth is deceptive—it begins slow and steady and is hard to differentiate from linear growth. Hence, predictions based on the expectation of an exponential pace can seem improbable.
Ray Kurzweil gives this example: “When the human genome scan got underway in 1990 critics pointed out that given the speed with which the genome could then be scanned, it would take thousands of years to finish the project. Yet the fifteen-year project was completed slightly ahead of schedule, with a first draft in 2003.”
Here’s a great visual of exponential growth’s deceptive then explosive nature in computers. See how most of the progress happens right at the end after years of doubling?
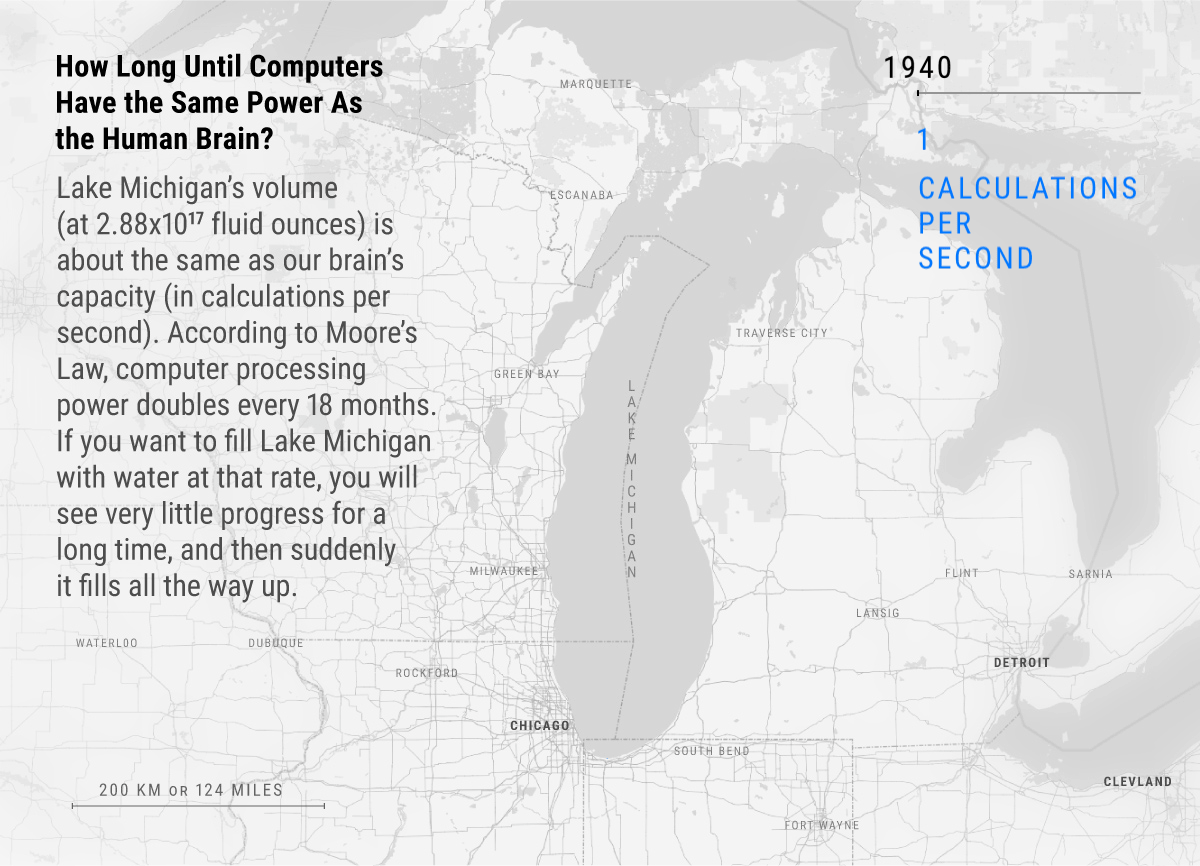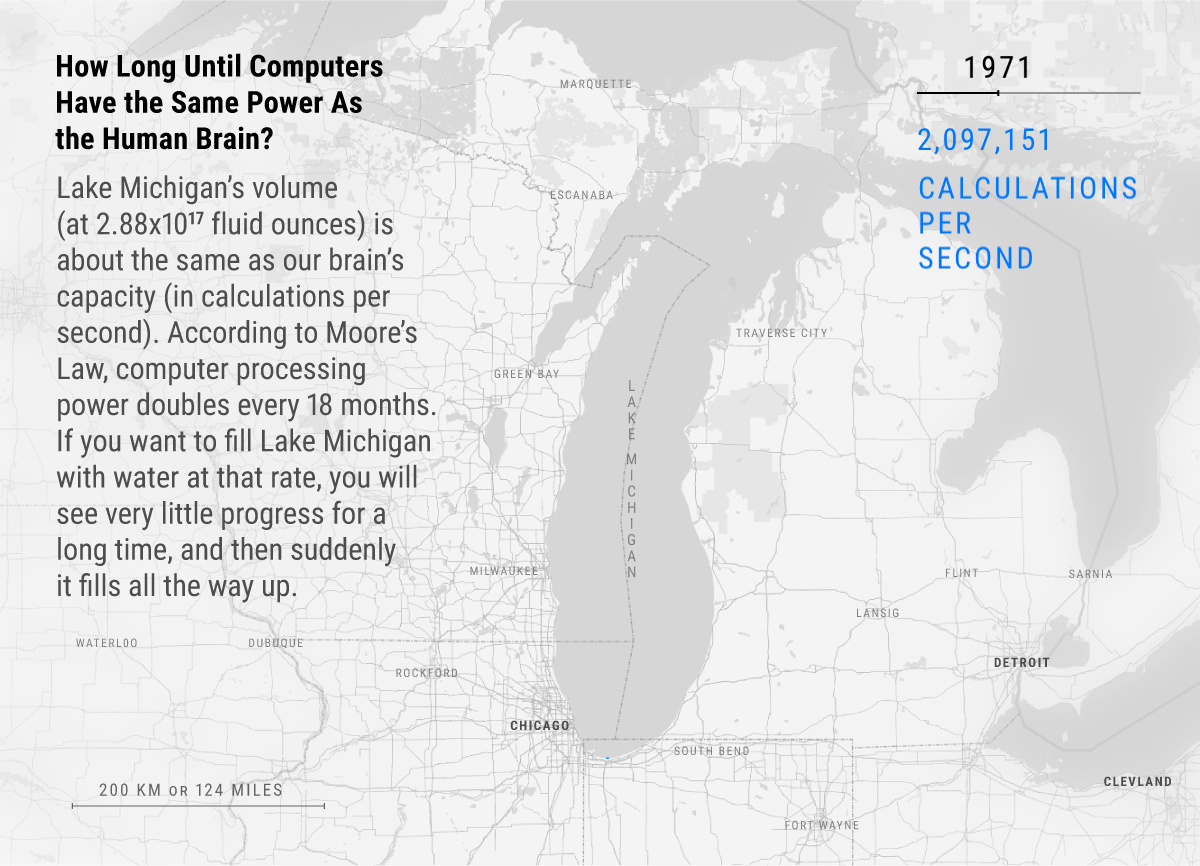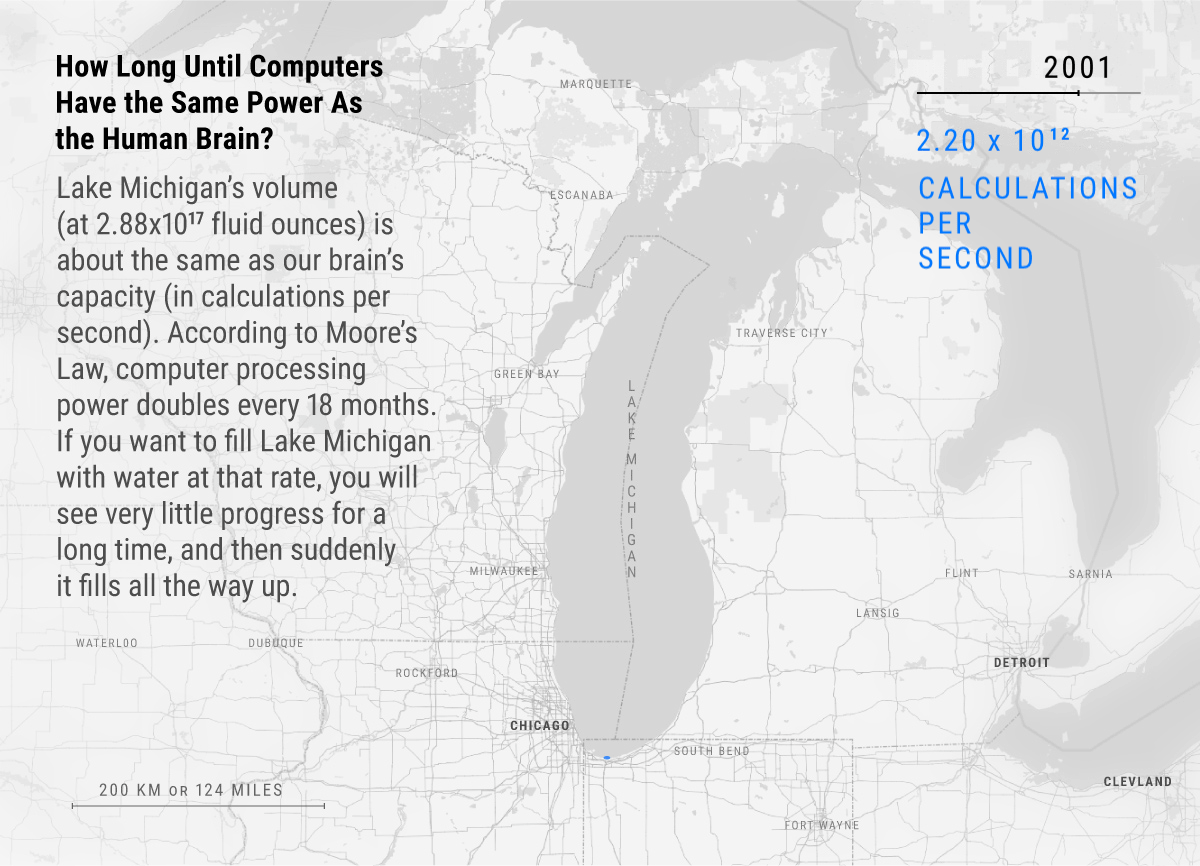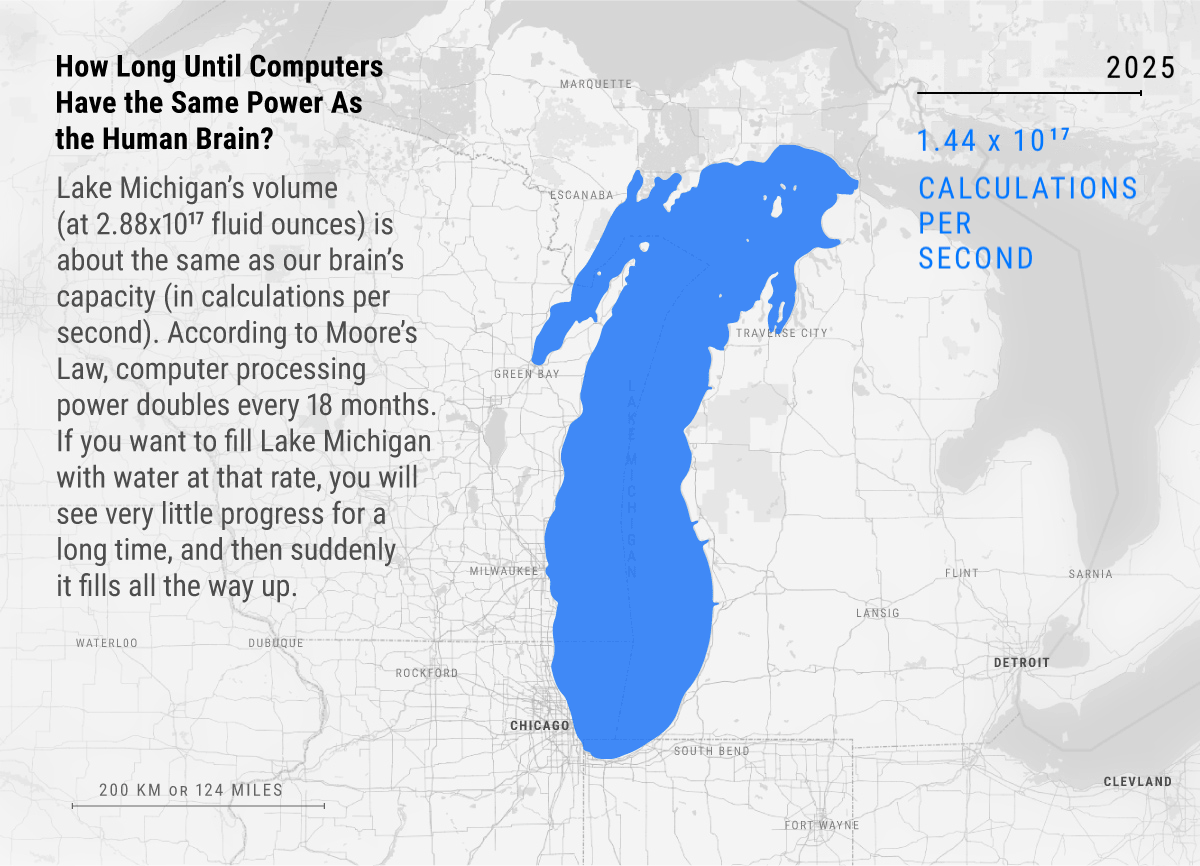
Will exponential growth eventually end?
In practice, exponential trends do not last forever. However, some trends can continue for long periods, driven along by successive technological paradigms.
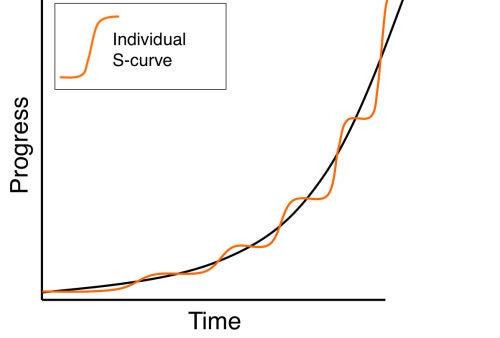
A broad exponential trend, computing for example, is made up of a series of consecutive S-shaped technological life cycles, or S-curves.
Each curve looks like the letter ‘S’ because of the three growth stages it represents—initial slow growth, explosive growth, and leveling off as the technology matures. These S-curves overlap, and when one technology slows, a new one takes over and speeds up. With each new S-curve, the amount of time it takes to reach higher levels of performance is less.
Kurzweil lists five computing paradigms in the 20th century: electromechanical, relay, vacuum tubes, discrete transistors, and integrated circuits. When one technology exhausted its potential, the next took over making more progress than its predecessors.
Planning for an exponential future
“[T]he future will be far more surprising than most people realize, because few observers have truly internalized the implications of the fact that the rate of change itself is accelerating.” Ray Kurzweil, The Singularity Is Near
The rule of thumb here is: expect to be surprised, then plan accordingly.
For example, what might the next five years look like? One way to forecast them would be to look at the last five and extend this pace forward. By now, the problem with this thinking should be clear: The pace itself is changing.
A better forecast would be to look at the last five and then reduce the time it will take to make a similar amount of progress in the next five. It’s more likely that what you think will happen in the next five years will actually happen in the next three.
The practice of exponential thinking isn’t really about the ins and outs of how you plan—you know how to do that—it’s about better timing your plan (whatever it may be).
In fact, Kurzweil’s law of accelerating returns arose from very practical of origins.
“As an inventor in the 1970s, I came to realize that my inventions needed to make sense in terms of the enabling technologies and market forces that would exist when the inventions were introduced, as that world would be a very different one from the one in which they were conceived,” Kurzweil wrote in the Singularity Is Near.
With a little practice, we can all make better plans by becoming consciously aware of our intuitive, linear expectations and adjusting them for an exponential future.
Why is learning to think exponentially valuable?
This isn’t just an interesting concept—our linear brains can get us into real trouble.
Thinking linearly causes businesses, governments, and individuals to get blindsided by factors that trend to exponential growth. Big firms get disrupted by new competition; governments struggle to keep policy current; all of us worry our future is out of control.
Exponential thinking reduces some of this disruptive stress and reveals new opportunities. If we can better plan for the accelerating pace, we can ease the transition from one paradigm to the next, and greet the future in stride.
To learn more about the exponential pace of technology and Ray Kurzweil’s predictions, read his 2001 essay “The Law of Accelerating Returns” and his book, The Singularity Is Near.
Image Credit: Shutterstock



